The General Approach

Many of the above mentioned rule sets are formulated as Boolean rules or slight extensions of Boolean algebra. Therefore, algorithms from the area of Boolean logic and automated reasoning are well suited for solving the associated problems. LogicNG provides many algorithms to work with Boolean and pseudo-Boolean formulas; the most important ones for solving complex problems being a variety of solvers, namely SAT-, Cardinality-, and MaxSAT Solvers. These can decide the satisfiability of large Boolean formulas, compute configurations, explain conflicts, and optimize solutions for given criteria. Alternatively, one can compile the problem into a knowledge compilation format like binary decision diagrams (BDD) or disjunctive negation normal forms (DNNF), and then perform computations on this compiled format. This general process is presented in the next figure.

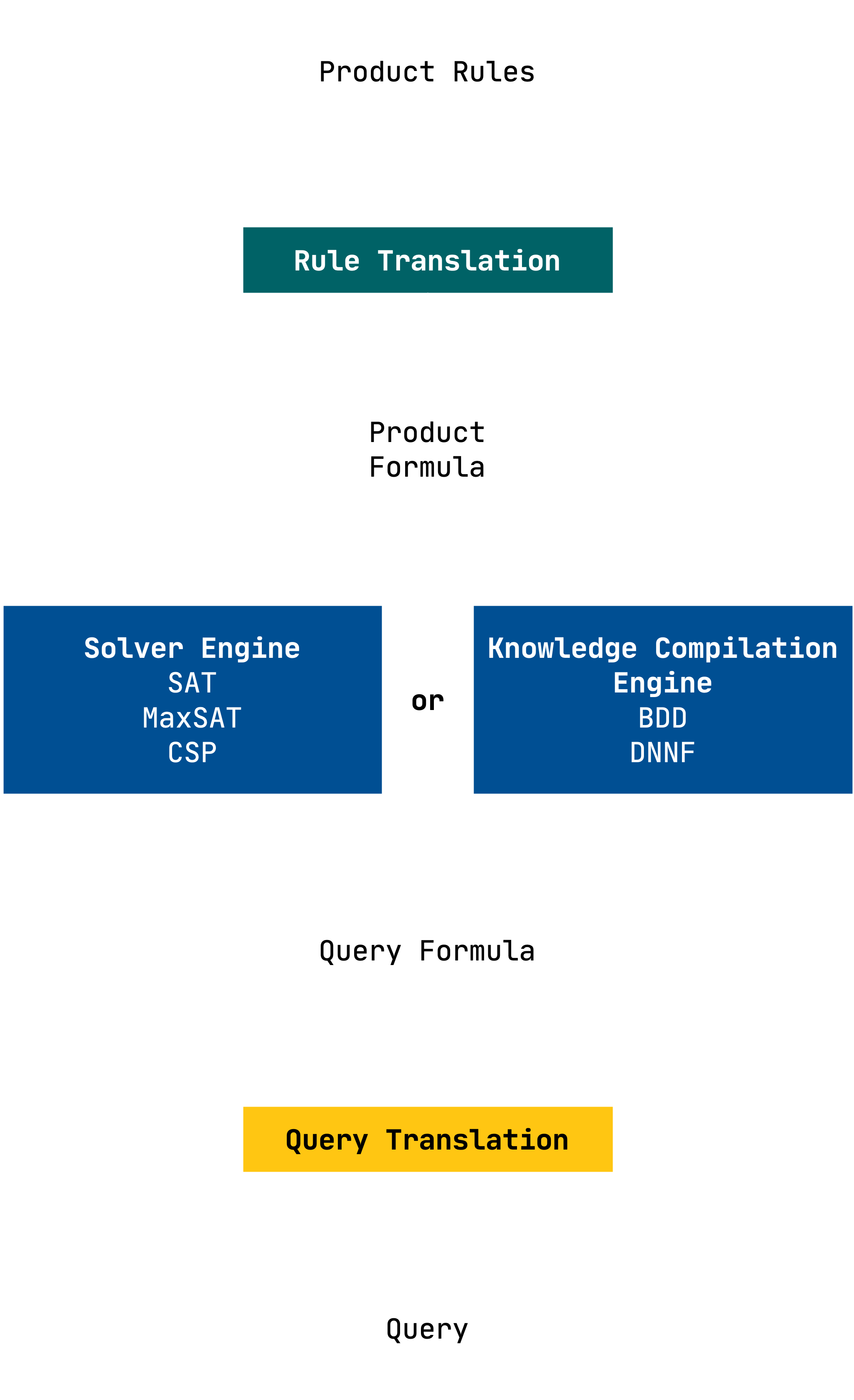
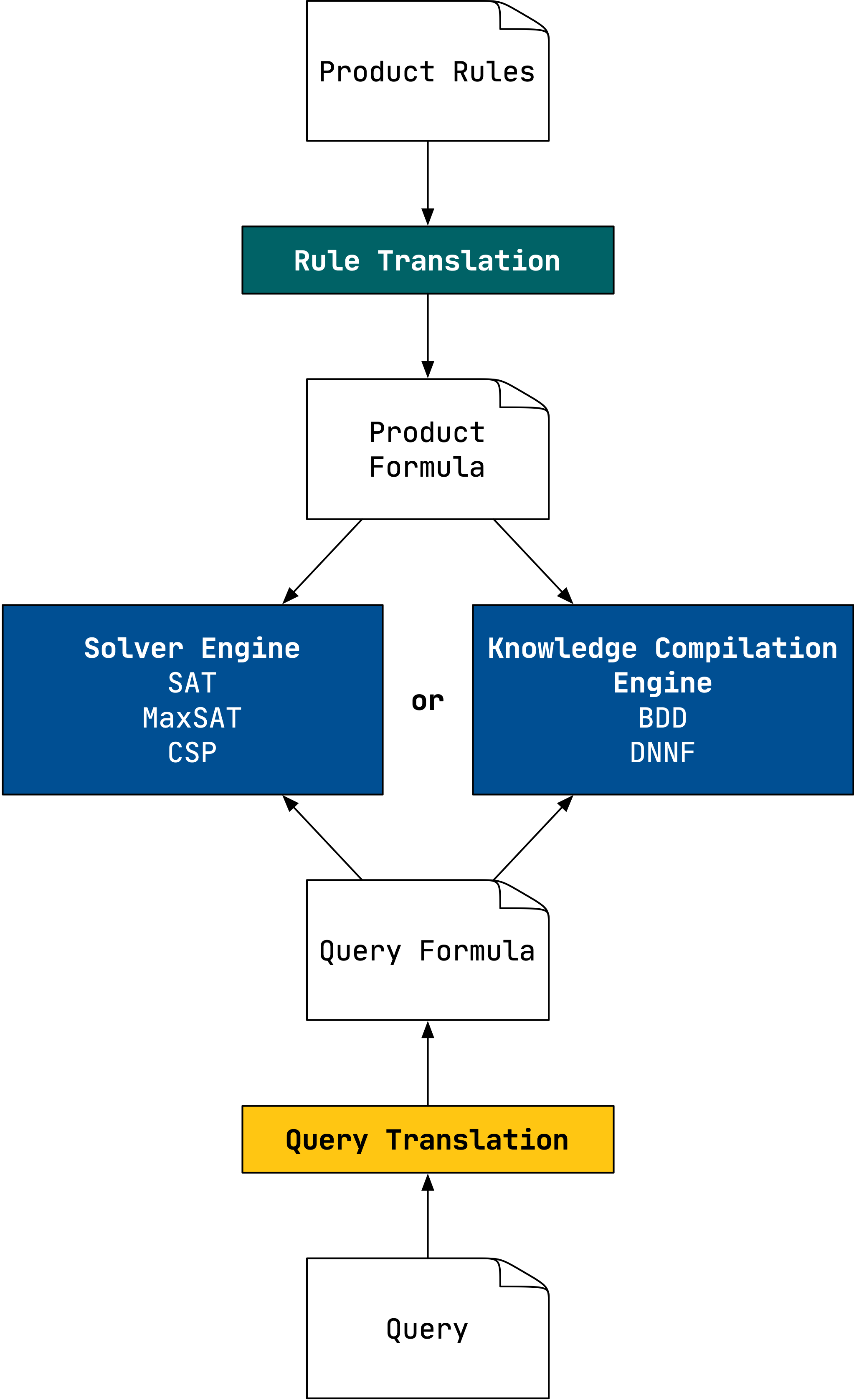
The product rules are translated to a Boolean formula, describing the entire solution space. I.e., each solution of this formula is one valid configuration of the product. This product formula is then either loaded onto a solver, or compiled into a knowledge compilation format. These two steps are usually performed only once, and then hundreds, thousands, or sometimes millions of requests are queried against the solver or compiled format.

To do this, the concrete query is also translated into a Boolean formula - the query formula - and then checked against the solver or compiled format. To illustrate this, imagine a vehicle as a product. All product rules are added onto a solver such that each solution found by the solver represents one valid vehicle configuration. Now take as an example the bill of material for this vehicle. For a premium car, typically, there are hundreds of different physical steering wheels, each with its own selection condition specifying in which vehicle the respective steering wheel is used. The question now is, whether there exists any valid vehicle which does not feature a steering wheel. The translation of this query into a Boolean formula is the conjunction of all possible steering wheels negated. If this query formula is satisfiable together with the product formula on the solver, then there is at least one vehicle which satisfies all product rules, but on the other hand does not satisfy any selection condition of a steering wheel - therefore we found a vehicle without steering wheel. If the product formula and the query formula are not satisfiable together, then we now know that each valid vehicle configuration indeed has a steering wheel.

LogicNG does not only provide the solvers and knowledge compilers, but also very efficient data structures for formulas, plus many algorithms to generate and manipulate these formulas. This is especially important for implementing product and query translators.